Sistemas de numeracion

SISTEMAS DE NUMERACIÓN

¿Que es un sistema de numeración?

es el conjunto de reglas y símbolos utilizados para representar datos numericos, se caracteriza fundamentalmente por su base y el numero distinto del numero que utiliza.

¿Como se identifican?

se pueden representar de manera donde: 

•  Es el sistema de numeración considerado (decimal, binario, hexadecimal, etc).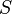
•   Es el conjunto de símbolos permitidos en el sistema, En el caso del sistema decimal son {0,1...9}; en el binario son {0,1}; en el octal son {0,1...7); en le hexadecimal son {0,1...9,A,B,C,D,E,F}.
•  Son las reglas que nos indican qué números y qué operaciones son válidos en el sistema, y cuáles no. En un sistema de numeración posicional las reglas son bastante simples, mientras que la numeración romana requiere reglas algo más elaboradas.

Clasificación:

1. En los sistemas de numeración no-posicionales los dígitos tienen el valor del símbolo utilizado, que no depende de la posición(columna) que ocupan en el numero.
2. En los sistemas de numeración ponderados o posicionales el valor de un dígito depende tanto del símbolo utilizado, como de la posición que ese símbolo ocupa en el número.

Sistemas de numeración posicionales conoce como base del sistema de numeración. si un sistema de numeración posicional tiene base b significa que disponemos de b símbolos diferentes para escribir los números, y que b  unidades forman una unidad de orden superior.

Ej: Si contamos desde 0,  incrementando una unidad cada vez, al llegar a 9 unidades hemos agotado los símbolos disponibles, y si que queremos seguir contando no disponemos de un nuevo símbolo para representar la cantidad que hemos contado. por tanto añadimos una nueva columna a la izquierda del numero, realizamos los símbolos que disponemos, decimos que tenemos una unidad de segundo orden ( decena), ponemos a cero las unidades, y seguimos contando

Conversión entre sistemas numericos: 

Decimal(10 dígitos)= 0,1,2,3,4,5,6,7,8,9

Binario(2 dígitos)=0,1

Octal (8 dígitos) = 0,1,2,3,4,5,6,7

Hexadecimal (16 dígitos) = 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

conversión de binario a decimal:

para poder transformar números binarios en su correspondiente decimal basta multiplicar el dígito binario (que solo puede ser 0 o 1) por 2 elevado a la potencia correspondiente según la cantidad de dígitos de la cifra. luego se suman los valores obtenidos y se consigue el numero final.

Ejemplo 

100011= 1*2^5+0*2^4+0*2^3+0*2^2+1*2^1+1*2^0=

32+0+0+0+2+1=

35

Conversión de Decimal a Binario:

para convertir un numero decimal a otro sistema el numero decimal es sucesivamente dividido por la base del sistema, en este caso la base del sistema binario es 2 el numero sera sucesivamente dividido entre 2 y el resultado del cociente sera nuevamente dividido y así sucesivamente hasta que el cociente sea 0. El resto de cada división es un numero binario que conforma el numero resultante de la conversión. El primer resultado producido (el primer resto obtenido) corresponde al bit mas próximo al punto decimal ( o lo que se conoce como bit de menor peso). Los sucesivos bits se colocan a la izquierda del anterior. Déjese notar que esto es como escribir en sentido contrario al empleado normalmente

Ejemplo:

20

20/2= 10 Residuo=0

10/2 = 5 Residuo=0

5/2=  2 residuo =__1

2/2= 1 Residuo=__0

1/2= ?Residuo __1

El 1 ya no se puede dividir entre 2 pero se coloca el 1

20= 10100

Conversión de Decimal a Octal:

en este caso basta usar el mismo método de conversión con los números binarios. Pero en vez de hacer divisiones sucesivas entre 2 hay que efectuarlas entre 8. Notese que el divisor corresponde a la base del sistema al cual se va a convertir.

Ejemplo

125(Octal)

125/8= 15 Residuo = 5

15/8= 1 Residuo= __7

1/8 =0 Residuo =__1

125(octal) = 175(decimal)

Sistema Hexadecimal

Este sistema requiere el uso de 16 símbolos, siendo formado por los mismos empleados en el sistema decimal y seis letras del alfabeto comprendida entre A y F.

Conversión de hexadecimal a Binario:

para efectuar la conversión basta con colocar los cuatro bits correspondientes a cada símbolo del numero hexadecimal

Ejemplo

4B2= 4 11 2

4=0100

11=1011

2=0010

4B2= 0100 1011 0010

Conversión de binario a hexadecimal:

para efectuar esta conversion hay que agrupar los bits de acuatro comenzando con los primeros 4 bits de la izquierda siguendo con los bits de la derecha

Ejemplo:

011011010101 = 0110 1101 0101

0110=___4

1101=13=D

0101=__5

0110 1101 0101 = 4D5